堆

什么是堆

堆本质上是一种特殊的树结构————完全二叉树，且堆中每个节点的值都大于其子节点的值。
因此分为 大根堆 / 小根堆

堆的表示

可以用数组来表示。
当前节点序号为i，其子节点为 i * 2 + 1 、 i * 2 + 2
当前节点序号为i，其父节点为 Math.floor(i/2) // 向下取整

堆中的一系列操作

建堆

自顶向下（nlogn）
不断将数据插入堆尾，然后每插入一次进行一次堆化操作（也就是上浮操作）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const arr = [7, 4, 1, 2, 9, 6, 5, 8]

function heapifyUp(arr) {
    for (let i = arr.length - 1; i > 0; i--) {
        let j = i
        while (arr[j] > arr[Math.floor(j / 2)]) {
            // 交换两个节点
            let t = arr[j]
            arr[j] = arr[Math.floor(j / 2)]
            arr[Math.floor(j / 2)] = t
            j = Math.floor(j / 2)
        }
    }
    return arr
}

自下而上（n）
将数组从第一个非叶子节点开始，对其子树进行下沉操作进行堆化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const arr = [7, 4, 1, 2, 9, 6, 5, 8]
function createHeap(arr) {
    const len = arr.length
    // 下沉操作
    function down(i) {
        while (i < len) {
            left_index = 2 * i + 1
            right_index = 2 * i + 2
            if (left_index >= len) return
            let index = arr[left_index] > arr[right_index] ? left_index : (arr[right_index] ? right_index : left_index)
            let t = arr[i]
            arr[i] = arr[index]
            arr[index] = t
            i = index
        }
    }
    for (let i = len / 2 - 1; i >= 0; i--) {
        down(i)
    }
    return arr
}



console.log(createHeap(arr));

堆化（将数组转化为堆结构）

堆化主要分为两种，上浮和下沉
上浮：
从右往左，如图：
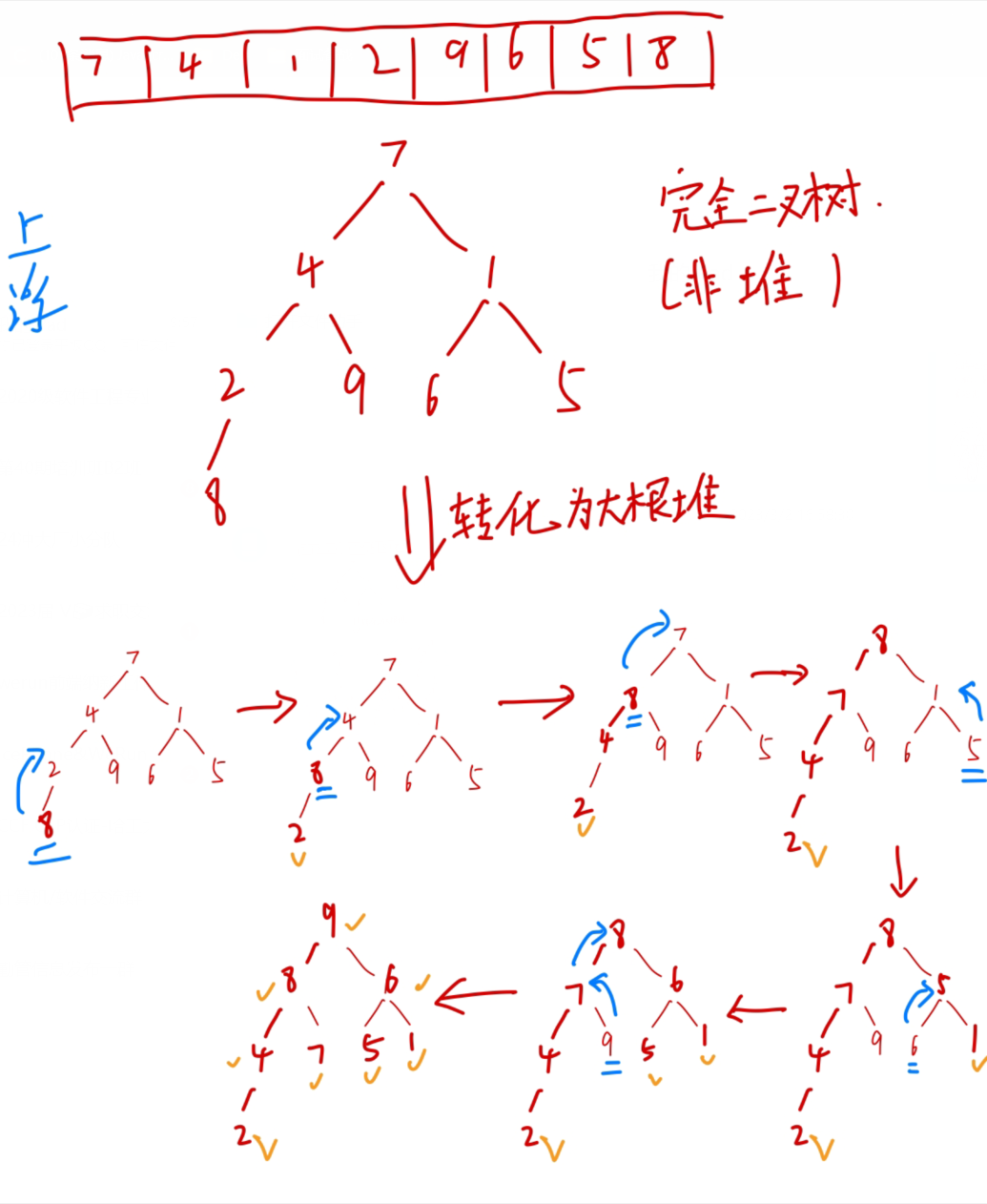
ppA2F81.png
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const arr = [7, 4, 1, 2, 9, 6, 5, 8]

function heapifyUp(arr) {
    for (let i = arr.length - 1; i > 0; i--) {
        let j = i
        while (arr[j] > arr[Math.floor(j / 2)]) {
            // 交换两个节点
            let t = arr[j]
            arr[j] = arr[Math.floor(j / 2)]
            arr[Math.floor(j / 2)] = t
            j = Math.floor(j / 2)
        }
    }
    return arr
}

插入

先插入到数组尾部，确保数据结构为完全二叉树，然后再进行堆化。
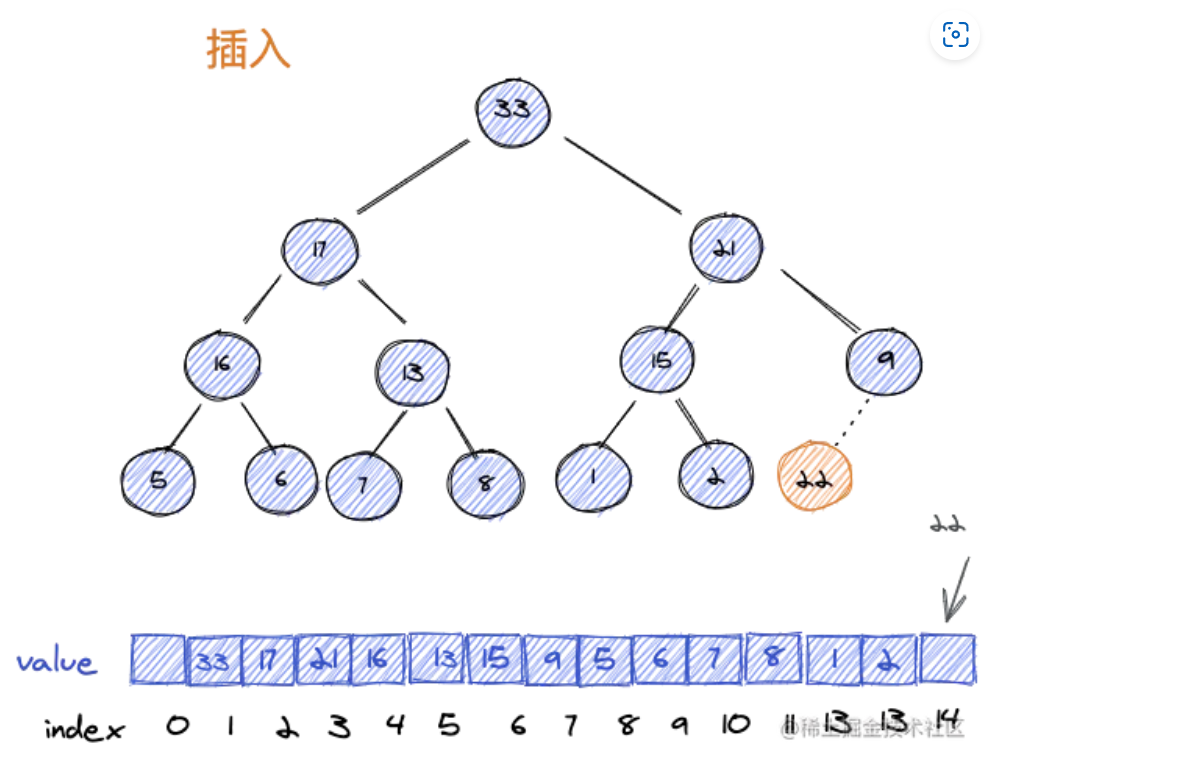
ppA20Gn.png
代码：

1
2
3
4
5
6
7
8
9
10
11
12
function insert(number, heap) {
    heap.push(number)
    let index = heap.length - 1, father_index = Math.floor(index / 2)
    while (heap[index] > heap[father_index]) {
        let t = heap[index]
        heap[index] = heap[father_index]
        heap[father_index] = t
        index = father_index
        father_index = Math.floor(index / 2)
    }
    return heap
}

删除堆顶元素

先将堆顶元素与末尾元素进行交换，（以大根堆为例），再将堆顶元素进行下沉操作。

与堆有关的时间复杂度

堆化：O(logn)
插入：O(logn)
删除：O(logn)

堆排序

堆排序的基本思想是：
1.将待排序序列构造成一个大顶堆
2.此时，整个序列的最大值就是堆顶的根节点。
3.将其与末尾元素进行交换，此时末尾就为最大值。
4.然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。